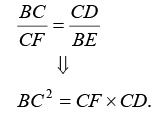Решение задач с помощью уравнений.
Скачать:
Предварительный просмотр:
Подписи к слайдам:
Индийская Наука Значение индийской науки для Запада невозможно переоценить. Большинство великих открытий и изобретений, которыми гордится Европа, были бы невозможны без созданной в Индии математической системы. Если говорить о влиянии, которое оказал на мировую историю неизвестный математик, изобретший новую систему, и о его аналитическом даре, его можно считать самым значительным после Будды человеком, которого когда-либо знала Индия. Средневековые индийские математики, такие как Брахмагупта (VII в.), Махавира (IX в.), Бхаскара (XII в.), в свою очередь, сделали открытия, которые стали известны в Европе только в эпоху Ренессанса и позднее. Они оперировали положительными и отрицательными величинами, изобрели изящные способы извлечения квадратного и кубического корней, они умели решать квадратные уравнения и некоторые типы неопределенных уравнений.
Условия Задачи Цветок лотоса возвышался над поверхностью пруда на 4 фута. Под напоров ветра он скрылся под водой на расстоянии 16 футов от того места, где он раньше поднимался над водой. Какой глубины был пруд ?
Решение Обозначим глубину пруда через х , тогда высота лотоса будет (х+4). Когда подул ветер, высота лотоса превратилась в гипотенузу прямоугольного треугольника, одна из сторон которого х (глубина пруда), другая — 16. По теореме Пифагора: х 2 + 16 2 = (x+4) 2 x 2 + 256 = x 2 +8x+16 8x+16=256 8x=240 x=30.
Источник
Задача бхаскары цветок лотоса возвышался над поверхностью
Одним из самым парадоксальным примеров среди решений задач с пифагоровыми тройками – это решение американского изобретателю многочисленных математических и шахматных головоломок Сэма Ллойда, он решает задачу У.Лонгфелло из романа «Каванаг» по своему.
Условие из романа: цветок лотоса возвышается над поверхностью озера на 2 пяди дюймов, а максимальное отклонение равно локтю, т.е. 21 дюйму. Надо также найти глубину озера. Ответ:17,05 дюйма.
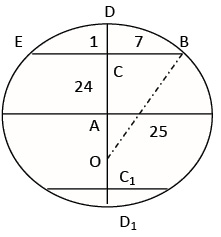
Треугольник Лонгфелло-Ллойда имеет параметры (21; 17,05; 27,05) или умножив на 20 получим треугольник в целых числах — (341,420,541), где 341 и 541 — простые числа, а 420 кратно 60, т.е. делится одновременно на 3,4,5.
Удивительно, но эти целочисленные параметры получаются непосредственно из формул, при m=21, n=10:
В матрице много пустых клеток, которые являются следствием общей теоремы о пифагоровых тройках чисел.
Если m=5 и n=1, то a=24, b=10, c=26.
Современная французская версия задачи «О лотосе» дана в книге М. Беррандо как задача «О нефтяной вышке».
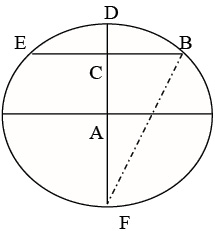
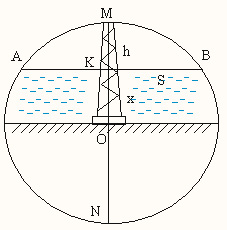
В Северном море установили на тяжелой бетонной платформе, закрепленной на дне моря, нефтяную буровую вышку. Она возвышалась над гладью воды на h=40 м. Во время сильного шторма вышка опрокинулась. Катастрофа была заснята с соседней платформы, причем было замечено, что вышка исчезла в пучине в s=84 м от точки, где прежде поднималась вышка. Чему равна глубина в этом месте?
Легко заметить, что пара чисел из условия задачи (40,84) пропорциональны паре (10,21) из задачи Лонгфелло. Отсюда естественный вывод, что глубина моря, где стояла нефтяная вышка, равна: 4×17,05=68,2 (метра).
Заключение. Теорема Пифагора как фундаментальный факт обладает значительным дидактическим ресурсом обновления содержания образования в 5-6 классах, позволяющим органично связать теорему с понятием простого и составного числа, признаками делимости на 3, 4, 5, введением понятия подобия геометрических фигур в начальный курс математики 5 и 6 классов. Это может в действительности стать основой интегративного курса математики, объединяющего геометрические и алгебраические компоненты единого математического знания.
По аналогии с американской версией задачи «о лотосе» можно составить задачу о камыше.
Алгебраически при m=7 b n=1 получим:
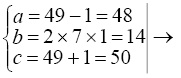
В учебнике для 8-го класса П.М. и О.П. Эрдниевых вводится признак Пифагора (упоминался ранее в работах Мордухай-Ботовского).
Если a 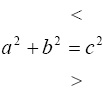
Источник
Решение задач с помощью уравнений. — презентация
Презентация была опубликована 7 лет назад пользователемЭдуард Арзамасцев
Похожие презентации
Презентация на тему: » Решение задач с помощью уравнений.» — Транскрипт:
2 Индийская Наука Значение индийской науки для Запада невозможно переоценить. Большинство великих открытий и изобретений, которыми гордится Европа, были бы невозможны без созданной в Индии математической системы. Если говорить о влиянии, которое оказал на мировую историю неизвестный математик, изобретший новую систему, и о его аналитическом даре, его можно считать самым значительным после Будды человеком, которого когда-либо знала Индия. Средневековые индийские математики, такие как Брахмагупта (VII в.), Махавира (IX в.), Бхаскара (XII в.), в свою очередь, сделали открытия, которые стали известны в Европе только в эпоху Ренессанса и позднее. Они оперировали положительными и отрицательными величинами, изобрели изящные способы извлечения квадратного и кубического корней, они умели решать квадратные уравнения и некоторые типы неопределенных уравнений.
3 Условия Задачи Цветок лотоса возвышался над поверхностью пруда на 4 фута. Под напоров ветра он скрылся под водой на расстоянии 16 футов от того места, где он раньше поднимался над водой. Какой глубины был пруд ?
4 Решение Обозначим глубину пруда через х, тогда высота лотоса будет (х+4). Когда подул ветер, высота лотоса превратилась в гипотенузу прямоугольного треугольника, одна из сторон которого х (глубина пруда), другая По теореме Пифагора: х = (x+4) 2 x = x 2 +8x+16 8x+16=256 8x=240 x=30.
Источник
Старинные задачи для учащихся 8 класса
Квадратные уравнения
1. Индусская задача из Бхасхары (1114г.).
Квадрат пятой части обезьян, уменьшенной на три, спрятался в гроте; одна обезьяна, влезшая на дерево, была видна. Сколько было обезьян?
2. Индусская задача из Бхасхары (1114г.).
Цветок лотоса возвышался над поверхностью пруда на четыре фунта, под напором ветра он скрылся под водой на расстоянии 16 футов от того места, где он раньше поднимался над водой. Какой глубины был пруд?
3. Индусская задача из Бхасхары (1114г.).
Часть восьмая их в квадрате
Криком радостным двенадцать
Вместе сколько, ты мне скажешь,
4. Задача Безу (XVIII в.).
Некто купил лошадь и спустя некоторое время продал её за 24 пистоля. При этом он потерял столько процентов своих денег, сколько стоила ему лошадь. За какую сумму денег была куплена лошадь первоначально?
5. Задача Маклорена (XVIIIв.).
Несколько человек обедали вместе и по счёту должны уплатить 175 шиллингов. Так как у двоих из них денег не оказалось, каждому из оставшихся пришлось уплатить на 10 шиллингов больше. Сколько человек обедало?
6. Эту задачу предложили в 1834 г. Ване Петрову в Костромской гимназии, учителя которой решили проверить слух о необыкновенных способностях Вани. Ему предложили 12 задач, на решение которых у него 1 ч 17 мин, причем значительная часть времени была использована для чтения и повторения задач, так как он не только не умел читать, но и писать. Ваня решал каждую задачу единственно силою соображения и памяти. Эту задачу Ваня решал подбором, удерживая в памяти все числа. Московский профессор Д.М. Перевощиков никак не ожидал, что мальчик решит задачу, которую мы бы решали способом составления квадратного уравнения:
За 500 рублей куплено несколько пудов сахара. Если бы на те же деньги купили на 5 пудов больше, то каждый пуд обошёлся бы на 5 руб. дешевле. Сколько куплено сахару?
7. Из «Книги абака» Фибоначчи (1180-1240 гг.).
8. Из «Науки о числах в трёх частях» Николая Шюке (XV в.).
Теорема Пифагора
9. Из «Арифметики» Магницкого (1703 г.).
Случися некоему человеку к стене лестницу прибрати, стены же тоя высота 117 стоп. И обреете лестницу долготою 125 стоп. И ведати хощет, колико стоп сея лестницы нижний конец от стены отстояти имать.
10. Из старинного руководства (1200 г.).
Две башни в равнине находятся на расстоянии 60 локтей одна от другой. Высота одной из них – пятьдесят локтей, высота другой – сорок локтей. Между башнями находится колодец, одинаково удалённый от вершин обеих башен. Спрашивается, как далеко находится колодец от основания каждой башни.
11. Индусская задача из Бхасхары (1114 г.).
На самом берегу ручья растет тополь. Порыв ветра сломил его на высоте трех единиц от земли, и он упал перпендикулярно к направлению ручья, ширина которого равна четырем единицам длины; при падении дерево уперлось в край противоположного берега. Как высок был тополь?
12. Старинная индийская задача.
Над озером тихим с полфута над водой
Он рос одиноко, и ветер волной
Нагнул его в сторону, — и уж нет
В двух футах от места, где рос.
Сколь озера здесь вода глубока? –
13. Задача древнекитайского ученого Цзинь Киу-чау (1250 лет до н.э.).
В центре квадратного пруда, имеющего 10 футов в длину и ширину, растет тростник, возвышающийся на 1 фут над поверхностью воды. Если его пригнуть к берегу, к середине пруда, то он достигнет своей верхушкой берега. Какова глубина пруда?
14. Задача древнекитайского ученого Цзинь Киу-чау (1250 лет до н.э.).
Бамбуковый ствол в 9 футов высотой переломлен бурей так, что если верхнюю часть его нагнуть к земле, то верхушка коснется земли на расстоянии 3 футов от основания ствола. На какой высоте переломлен ствол?
РЕШЕНИЯ, УКАЗАНИЯ, ОТВЕТЫ
Пусть х футов – глубина пруда.
По теореме Пифагора: х2 + 162 = (х + 4)2
Пусть х руб. стоила лошадь. По условию потерял х %, то есть руб.
Известно, что продал её за 24 рубля. Значит, лошадь стоила Имеем уравнение:
Ответ: за 60 или 40 рублей.
Пусть х шиллингов стоил обед, (х + 10) шиллингов стали платить за один обед, человек уплатили. Имеем уравнение:
Пусть х руб. стоил 1 пуд, пудов куплено, (х – 5) руб. стал бы стоить пуд, пудов купили бы. Имеем уравнение:
По теореме Пифагора: (стопы).
Пусть х локтей – от одной башни, (60 – х) локтей – от другой.
Источник
Олимпиадные задания по математике(УДЕ)
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике(УДЕ)
1. Расставьте знаки арифметических действиях и, если нужно, скобки так, чтобы равенства стали верными:
а) Муравей проехал на гусенице некоторое расстояние за 28 минут. За сколько минут муравей проедет на жуке расстояние в 4 раза большее, если скорость жука в 7 раз больше скорости гусеницы?
б) Составить и решить обратную задачу по схеме: □ мин,4, 7, 16мин
3. Можно ли разложить гири в 1, 2, 3, …, 21 граммов на две равные по весу кучи? Ответ объясните.
4. Решите ребус, заменяя одинаковые буквы одинаковыми цифрами:
5. Найдите площадь заштрихованной фигуры (сторона клетки равна 1 см)
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике(УДЕ)
1. Решите числовой ребус АХ+УХ=УРА (одинаковые буквы выражают одинаковые цифры).
а) Одна снегоуборочная машина могла бы убрать всю улицу за 1 час, а другая за 45 минут. Начав работу одновременно, машины проработали вместе 20 минут, после чего первая сломалась. Через сколько минут вторая машина закончила работу?
б) Составьте и решите обратную задачу по схеме: □, 45 ,20, 10.
3. Предположим, что сейчас угол между часовой и минутной стрелкой такой же, каким он был два часа назад. Чему равен этот угол?
4. Расставьте скобки в выражении -1=0 так, чтобы получилось верное равенство.
5. Найдите площадь заштрихованной фигуры (сторона клетки равна 1 см)
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике(УДЕ)
1. Футбольный мяч сшит из 32 лоскутков: белых шестиугольников и чёрных пятиугольников. Каждый чёрный лоскут граничит только с белыми, а каждый белый — с тремя чёрными и тремя белыми. Сколько лоскутов белого цвета?
а) Борода Карабаса-Барабаса составляла 40% его веса. После того, как Буратино её обрезал, она стала составлять 10% его веса. Какую часть бороды обрезал Буратино?
б) Составьте и решите обратную задачу по схеме: 40%,□, 5/6
3. У Пюрви на дне рождения было 5 друзей. Первому он отрезал 1/6 часть пирога, второму — 1/5 остатка, третьему — 1/4 того, что осталось, четвертому — 1/3 нового остатка. Последний кусок Пюрвя разделил пополам с пятым другом. Кому достался самый большой кусок?
4. На доске были написаны числа 1, 3, 4, 6, 8, 9, 11, 12, 16. Очир и Батыр стерли по четыре числа, и оказалось, что сумма чисел, стертых Очиром втрое больше суммы чисел, стертых Батыром. Какое число могло остаться на доске? Ответ объясните.
5. Найдите площадь треугольника (сторона клетки равна 1 см)
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике (УДЕ)
1. Двузначное число N умножили на 2, у результата поменяли местами цифры и поделили на 2. Получили 92. Каким могло быть число N?
а) Велосипедист должен попасть в пункт назначения к определённому сроку. Если он поедет со скоростью 10 км/ч, он опоздает на один час, а если он поедет со скоростью 15 км/ч, то он приедет на один час раньше срока. С какой скоростью ему нужно ехать, чтобы приехать вовремя?
б) Составьте и решите обратную задачу по схеме: □, 15 , 12.
3. Квадрат 8×8 распилили на квадраты 2×2 и прямоугольники 1×4. При этом общая длина распилов оказалась равна 54. Сколько фигурок каждого вида получилось?
4. По дороге идут два туриста. Первый делает шаги на 10% короче и в то же время на 10% чаще, чем второй. Кто из туристов идет быстрее и почему?
5. Найдите площадь четырехугольника ABCD, изображенного на рисунке (сторона клетки равна 1 см).
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике (УДЕ)
1. Докажите, что n3+2n делится на 3 для любого натурального n.
а) Из бутылки, наполненной доверху глицерином, отлили 8 л. Затем долили бутылку водой и отлили 6 л смеси. После этого вновь долили бутылку водой. Определите вместимость бутылки, если известно, что в результате получили смесь, содержащую 68% глицерина.
б) Составьте и решите обратную задачу по схеме: 40, 8,6, □ %.
3. Батыр выложил на столе из цифр пятизначное число N, а затем еще четыре числа: сумма первых двух цифр числа N, сумму первых трех, первых четырех, наконец, сумму всех пяти цифр числа N. В итоге на столе оказались: одна цифра 1, шесть цифр 2, одна цифра 4, три цифры 6, две цифры 8. Чему равно число N? Объясните свой ответ.
4. Компания ребят пошла в лес за грибами. В итоге каждый собрал меньше трети, но больше пятой части того, что собрали остальные. Сколько было ребят?
5. Найдите площадь четырехугольника, изображенного на рисунке.
Муниципальный этап республиканской олимпиады школьников по технологии УДЕ академика РАО в у. г.
Олимпиадные задания по математике (УДЕ)
1. Докажите, что при любом натуральном n выполняется равенство
а) Из бутылки, наполненной доверху глицерином, отлили 8 л. Затем долили бутылку водой и отлили 6 л смеси. После этого вновь долили бутылку водой. Определите вместимость бутылки, если известно, что в результате получили смесь, содержащую 68% глицерина.
б) Составьте и решите обратную задачу по схеме: 40, 8,6, □ %.
3. Задача Бхаскары (индийский математик XII в.): «Цветок лотоса возвышался над поверхностью пруда на 4 фута. Под напором ветра он скрылся под водой на расстоянии 16 футов от того места, где он раньше поднимался над водой. Какой глубины пруд?».
4. Прямая пересекает график функции y=x2 точках с абсциссами х1 и х2 , а ось абсцисс — в точке с абсциссой х3. Докажите, что
5. Существует ли треугольник с высотами, равными 1, 2 и 3? Ответ обоснуйте.
Источник